- I Formes quadratiques et formes polaires associées
- II Orthogonalité
- III Décomposition en carrés d'une forme quadratique
- IV Formes quadratiques sur un espace euclidien
- V Application: Coniques du plan affine euclidien
- VI Tous les exercices WIMS utilisés
- Index
Théorème
Démonstration
pour . Soit une base de , tout vecteur s'écrit , donc et alors car . On choisit dans ce cas
-
Premier Cas :
S'il existe tel que : pour fixer les idées, supposons que
Le principe est de regrouper tous les termes contenant et faire apparaître un début de carré.
Notons Remarquons que c'est une forme quadratique en .
On a
Soit alors et .est une forme quadratique sur un espace vectoriel de dimension , on lui applique alors l'hypothèse de récurrence. Les formes linéaires récupérées en utilisant l'hypothèse de récurrence sont nécessairement libres avec vu qu'elles n'ont pas de composantes suivant .
-
Deuxième Cas :
Cas où tous les sont nuls, la forme quadratique s'écrit alors sous la forme . Sans perte de généralité, supposons que .
L'idée est de regrouper tous les termes contenant et .
Posons,Remarquons que est un polynôme homogène de degré
en
.
est un polynôme homogène de degré
en
.
Une fois que c'est fait, on regroupe ces formes de la façon suivante:est une forme quadratique sur un espace vectoriel de dimension . En effet, le produit de deux formes linéaires est une forme quadratique.
En utilisant la relation , on obtient
Posonset
Les formes et sont deux formes linéaires indépendantes de et est une forme quadratique à qui on applique l'hypothèse de récurrence.
Remarque
Corollaire
Remarque utile
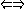 toutes les valeurs propres de
sont positives.
toutes les valeurs propres de
sont positives.
 la forme linéaire sur
la forme linéaire sur
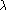 et
et
 de
.
Dans le repère
, on note
les composantes de
, alors il existe
tel
qu'une équation de
dans
soit
de
.
Dans le repère
, on note
les composantes de
, alors il existe
tel
qu'une équation de
dans
soit
 ,
on dit que
,
on dit que
 sont
sont